『正多面体と素数』の計算をしましょう(7)─正八面体・正二十面体と保型形式

• これは何
• はじめに
• 正八面体の場合
  • 正八面体多項式
  • 指標理論
  • 保型形式とテータ定数
  • Broué–Enguehard 写像 と重み枚挙多項式
  • レベル4の主合同部分群
• 正二十面体群の場合
  • 正二十面体方程式
  • ロジャース・ラマヌジャン恒等式
  • 正二十面体と保型形式
  • ラマヌジャンの連分数の特殊値
  • レベル5の主合同部分群
  • 分割数
• まとめと展望
• References

これは何

二項正 \(n\,(n=8,\,20)\) 面体の作用で高々 \(\pm 1\) の定数倍の変化しか受けない正 \(n\) 面体多項式と \(SL(2,\mathbb{Z})\) の保型形式は，主合同部分群に関する保型形式によって結びつく．この繋がりを紐解く過程で現れるのは，2元線形符号の重み枚挙多項式，ロジャース・ラマヌジャン恒等式，ラマヌジャンの連分数など、種々の興味深い数学的対象である．

前回の記事（本記事から GitHub Pagesで更新することにしました）

『正多面体と素数』の計算をしましょう(6)―正二十面体多項式と10n±1型整数

計算ノート等は以下のリポジトリに順次追加しています．

shironetsu/icosahedron

はじめに

本稿では

\[\begin{align} q = e^{2\pi i \tau} \end{align}\]

を約束する．最初にこれを宣言するのは，文献によって指数が \(\pi i\tau\) の場合と入り乱れているから．また，簡略記法として

\[\begin{align} \mathbf{e}(x) &= e^{2\pi ix},\hspace{12pt} x\in \mathbb{C} \end{align}\]

を導入する．これを用いると，\(q=\mathbf{e}(\tau)\) と書ける．1の原始 \(n\) 乗根の1つは \(\mathbf{e}(1/n)\) である．

正八面体の場合

正八面体多項式

これまでの記事では，正二十面体の対称性をもつ多項式，「正二十面体多項式」を考えてきた．同様の不変式は正八面体についても定義することができる．

正八面体の \(6\) つの頂点を単位球面上の \((\pm1,0,0),(0,\pm 1,0),(0,0,\pm1)\) に取ろう．各点は立体射影 \((x,y,z)\mapsto (x\!+\!yi)/(1\!+\!z)\)によって，

\[\begin{align} (1,0,0)&\mapsto 0,\\ (-1,0,0)&\mapsto \infty,\\ (0,1,0)&\mapsto 1,\\ (0,-1,0)&\mapsto -1,\\ (0,0,1)&\mapsto i,\\ (0,0,-1)&\mapsto -i \end{align}\]

へと写される．これら \(6\) つの像のうち，無限遠点を除いた \(5\) つを根に持つ \(X\) のモニック多項式は，

\[\begin{align} V_6(X) := X(X-1)(X+1)(X-i)(X+i) = X^5-X \end{align}\]

で与えられる．同次化して，同じ記号で2変数同次多項式 \(V_6(x,y)\)を定義する:

\[\begin{align} V_6(x,y) := y^6 V_6\left(\frac{x}{y}\right) = xy\,(x^4-y^4) \end{align}\]

\(V_6(x,y)\) のヘッセ行列式の定数倍から8次の\(V_8(x,y)\)を，\(V_6(x,y)\) と \(V_8(x,y)\) のヤコビ行列式の定数倍から \(V_{12}(x,y)\) をそれぞれ定義する．「定数倍」は\(x\) に関する最高次の項の係数が \(1\) となるように調整すると，

\[\begin{align} V_8(x,y) &= \frac{-1}{25} \begin{vmatrix} \dfrac{\partial^2 V_6}{\partial x^2} & \dfrac{\partial^2 V_6}{\partial x\partial y}\\ \dfrac{\partial^2 V_6}{\partial x\partial y} & \dfrac{\partial^2 V_6}{\partial y^2}\\ \end{vmatrix}\\ &= x^8+14x^4y^4+y^8\\ V_{12}(x,y) &= \frac{-1}{8} \begin{vmatrix} \dfrac{\partial V_6}{\partial x} & \dfrac{\partial V_6}{\partial y}\\ \dfrac{\partial V_8}{\partial x} & \dfrac{\partial V_8}{\partial y}\\ \end{vmatrix}\\ &= x^{12}-33x^8y^4-33x^4y^8+y^{12} \end{align}\]

となる．\(V_8(X,1)\) の根は， 「正八面体の8つの面の重心の（中心から外接球への射影の）立体射影による像」である．一方，\(V_{12}(X,1)\) の根は「正八面体の12個の辺の中点の（中心から外接球への射影の）立体射影による像」となる．

これら3つ，\(V_6,V_8,V_{12}\) を「基本正八面体多項式」と呼ぶことにしよう．\((1,\, 14,\, 1),\, (1,\,-33,\,-33,\,1)\) という係数の並びをなんとなく覚えておくと良い．

指標理論

まず，基本正八面体多項式たちが二項正八面体群による作用の下でどのように変化するか見よう．構成法からたかだか定数倍しか変化しないことは分かるが，真の意味で不変であることは保証されない．ところで，正八面体群 \(\cong\) \(4\)次対称群の指標表は以下で与えられる：

\[\begin{align} \begin{array}{|c|ccccc|} \hline \mbox{共役類} & e & \lbrack 13\rbrack & \lbrack 2^2\rbrack & \lbrack 1^22\rbrack & \lbrack 4\rbrack\\ \hline \# \mbox{共役類} & 1 & 8 & 3 & 6 & 6\\ \hline \theta & 0 & 2\pi/3 & \pi & \pi & \pi/2\\ \hline {\rm id} & 1 & 1 & 1 & 1 & 1\\ {\rm sgn} & 1 & 1 & 1 & -1 & -1\\ * & 2 & -1 & 2 & 0 & 0\\ * & 3 & 0 & -1 & 1 & -1\\ * & 3 & 0 & -1 & -1 & 1\\ \hline \end{array} \end{align}\]

Table 1. 正八面体群の指標表

1次元表現なら既約表現だから，正八面体群の1次元表現はTable 1.のちょうど2つだけある．一方が恒等表現（\(\rm id\)）で，もう一方は4次対称群の符号表現（\({\rm sgn}\)）に対応する．\(\varepsilon:=\mathbf{e}(1/8)\) とすると，\(\rho:(x,y)\mapsto(\varepsilon x, \varepsilon^{-1} y)\) が二項正八面体群に含まれるが，この作用によって基本正八面体多項式は

\[\begin{align} V_6(\varepsilon x, \varepsilon^{-1}y) &= - V_6(x,y),\\ V_8(\varepsilon x, \varepsilon^{-1}y) &= V_8(x,y),\\ V_{12}(\varepsilon x, \varepsilon^{-1}y) &= - V_{12}(x,y) \end{align}\]

と変化を受ける．\(\rho\) は正八面体群では \(z\) 次周りの\(90^\circ\)回転に対応して，4次対称群では互換（奇置換）に対応する．このことから，\(V_6,V_{12}\) は 符号表現に属し，\(V_8\) は恒等表現に属すことが分かる．

このあたり，単純群である正二十面体群とは事情が異なる．あとで登場するが，正二十面体多項式は二項正二十面体群の作用で定数倍を込めても不変になる．

次に，\(SO(3)\) の \((2j+1)\) 次元既約表現の，正八面体群 \(O\) への制限が恒等表現をいくつ含むか考える．

\(SO(3)\) の \((2j+1)\) 次元既約表現の指標を \(\chi_{j}\) で表す．\(SO(3)\) の共役類は，軸回りの回転角 \(\theta\) だけで決まって，\(g \in SO(3)\) に対して，

\[\begin{align} \chi_{j}(g) = \sum_{k=-j}^j e^{\sqrt{-1}j\theta} = 1+2\sum_{k=1}^j \sin(k\theta) \end{align}\]

で与えられる．Table 1.で正8面体群の各共役類の回転角を \(\theta\) の行に与えておいた．これを使うと，\(2j+1\) 次元表現における重複度 \(d_{\rm sgn}(j), d_{\rm id}(j)\) の母関数として，

\[\begin{align} g_{\rm id}(t) &= \sum_{j=0}^\infty d_{\rm id}(j)t^j\\ &= \sum_{j=0}^\infty \frac{1}{|O|} \sum_{g \in O}\chi_{j}(g)\chi_{\rm id}(g) t^j\\ &= \frac{1-t^{18}}{(1-t^4)(1-t^6)(1-t^9)},\\ g_{\rm sgn}(t) &= \sum_{j=0}^\infty d_{\rm sgn}(j)t^j\\ &= \sum_{j=0}^\infty \frac{1}{|O|} \sum_{g \in O}\chi_{j}(g)\chi_{\rm sgn}(g) t^j\\ &= \frac{t^3}{(1-t^3)(1-t^4)} \end{align}\]

が得られ，テイラー展開から，

\[\begin{align} d_{\rm id}(j) &= \left\{ \begin{aligned} &\left\lfloor\frac{j}{12}\right\rfloor+1, & j&\equiv 0,4,6,8,9,10 \mod 12,\\ &\left\lfloor\frac{j}{12}\right\rfloor & j&\equiv 1,2,3,5,7,11 \mod 12, \end{aligned} \right. \\ d_{\rm sgn}(j) &= \left\{ \begin{aligned} &\left\lfloor\frac{j}{12}\right\rfloor+1, & j&\equiv 3,6,7,9,10,11 \mod 12,\\ &\left\lfloor\frac{j}{12}\right\rfloor & j&\equiv 0,1,2,4,5,8 \mod 12. \end{aligned} \right. \end{align}\]

が分かる．最初のいくつかの値を表に示す．

\[\begin{align} \begin{array}{|c|ccccccccccccccccc|} \hline 2j & 0 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20 & 22 & 24 & 26 & 28 & 30 & \cdots\\\hline d_{\rm id}(j)& 1^* & 0 & 0 & 0 & 1^* & 0 & 1 & 0 & 1 & 1^* & 1 & 0 & 2^* & 1 & 1 & 1 & \cdots\\\hline d_{\rm sgn}(j)&0 & 0 & 0 & 1^* & 0 & 0 & 1^* & 1^* & 0 & 1 & 1^* & 1 & 1 & 1 & 1 & 2^* & \cdots\\\hline \end{array} \end{align}\]

Table 2. アスタリスクは「重根を持たない正八面体多項式」の数に付けている．詳細は別の記事にて．

さて，\(V_6^4,\,V_8^3,\,V_{12}^2\) の3つはともに \(2j=24\) の恒等表現に属すが，上の表によるとこの表現空間の次元は \(d_{\rm id}(12)=2\) しかないから，少なくとも1つ1次の関係式が存在しなくてはならない．実際に計算すると，

\[\begin{align} V_8(x,y)^3-V_{12}(x,y)^2 = 108V_6(x,y)^4 \end{align}\]

の関係が成り立つ．少し変形すると

\[\begin{align} \frac{V_8^3(x,y)-V_{12}^2(x,y)}{1728} = \left(\frac{V_6(x,y)}{2}\right)^4 \end{align}\]

…式(i)

という非常に象徴的な式が出現する．

保型形式とテータ定数

何が「象徴的」なのか．\(SL(2,\mathbb{Z})\) の保型形式について思い出そう．（規格化された）アイゼンシュタイン級数 \(E_4,\,E_6\) と デデキントのエータ関数 \(\eta\) は以下で定義される：

\[\begin{align} E_4(\tau) &= 1+240\sum_{n=1}^\infty\sigma_3(n)q^n,\\ E_6(\tau) &= 1-504\sum_{n=1}^\infty\sigma_5(n)q^n,\\ \eta(\tau) &= q^{1/24}\prod_{n=1}^\infty(1-q^n) \end{align}\]

ただし，\(\sigma_k(n)=\sum_{d \vert n}d^k\) は約数関数．ウェイト12の保型形式の次元に関する制約（上で行った正八面体の表現に関する議論とほとんどパラレルなものである）から，次の等式が成り立つことが知られている：

\[\begin{align} \frac{E_4(\tau)^3-E_6(\tau)^2}{1728} = \eta(\tau)^{24} \end{align}\]

…式(ii)

式(i)と式(ii)を見比べる．ここにはあまりにも明白な対応関係がある．期待されるのは，\(x,\,y\) に \(\tau\) に依存する何かを代入すれば，

\[\begin{align} V_8(x,y) &= E_4(\tau)\\ V_{12}(x,y) &= E_6(\tau)\\ V_6(x,y) &= 2\eta(\tau)^6 \end{align}\]

が成り立つこと．\(x,\,y\) には何を代入すればよいのだろうか？

答えはテータ定数である．

このことを見るためにヤコビのテータ定数について振り返る．テータ定数は

\[\begin{align} \begin{aligned} \theta_2(\tau) &= \sum_{n \in \mathbb{Z}} q^{(n+1/2)^2/2} &&=2q^{1/8}\prod_{n=1}^\infty (1-q^n)(1+q^n)^2,\\ \theta_3(\tau) &= \sum_{n \in \mathbb{Z}} q^{n^2/2} &&=\prod_{n=1}^\infty (1-q^n)(1+q^{n-1/2})^2,\\ \theta_4(\tau) &= \sum_{n \in \mathbb{Z}} (-1)^nq^{n^2/2} &&= \prod_{n=1}^\infty (1-q^n)(1-q^{n-1/2})^2 \end{aligned} \end{align}\]

によって定義される［Kharchev］．

\(PSL(2,\mathbb{Z})\) の生成元 \(T:\tau\mapsto \tau+1\) と \(S:\tau\mapsto -1/\tau\) による変換性はそれぞれ，

\[\begin{align} \theta_2(T\tau) &= \varepsilon \theta_2(\tau),\\ \theta_3(T\tau) &= \theta_4(\tau),\\ \theta_4(T\tau) &= \theta_3(\tau) \end{align}\]

および

\[\begin{align} \theta_2(S\tau) &= \sqrt{-i\tau}\, \theta_4(\tau),\\ \theta_3(S\tau) &= \sqrt{-i\tau}\, \theta_3(\tau),\\ \theta_4(S\tau) &= \sqrt{-i\tau}\, \theta_2(\tau),\\ \end{align}\]

によって与えられる．ただし，\(\varepsilon=\mathbf{e}(1/8)\)，\(\sqrt{-i\tau}\) は実部が正となるようにとる．個々のテータ定数は \(SL(2,\mathbb{Z})\) の保型形式ではない. しかし，これらをうまく組合せると， \(SL(2,\mathbb{Z})\) に関する保型性を持つようになる．

まず，無限乗積展開から，

\[\begin{align} \theta_2(\tau)\theta_3(\tau)\theta_4(\tau) &= 2q^{1/8}\prod_{n=1}^\infty (1-q^n)^3 = 2\eta(\tau)^3 \end{align}\]

が分かる．ちなみに

\[\begin{align} \eta(\tau)^3 = \sum_{n=0}^\infty (-1)^n (2n+1) q^{(2n+1)^2/8} \end{align}\]

はヤコビによる古典的な結果として知られている．これは \(SL(2,\mathbb{Z})\) の保型形式ではないが，\(8\) 乗した

\[\begin{align} \left(\frac{\theta_2(\tau)\theta_3(\tau)\theta_4(\tau)}{2}\right)^8 = \eta(\tau)^{24} = \Delta(\tau) \end{align}\]

はウェイト \(12\) の保型形式，特にラマヌジャンのデルタと呼ばれる，\(q\) に関する定数項のないカスプ形式になる．

次に，テータ定数をそれぞれ \(8\) 乗したものの和を \(f_8(\tau):= \theta_2^8(\tau) + \theta_3^8(\tau) + \theta_4^8(\tau)\) とすると，

\[\begin{gather} f_8(T\tau) = f_8(\tau),\hspace{12pt}f_8(S\tau) = \tau^4 f_8(\tau) \end{gather}\]

が成立する．これは \(f_8(\tau)\) がウェイト4の保型形式であることを意味する．フーリエ展開から分かるように定数項は \(2\) で，ウェイト \(4\) の保型形式は定数倍を除いてただ一つしか存在しないから，既に登場したウェイト \(4\) の保型形式であるアイゼンシュタイン級数 \(E_4\) とは

\[\begin{align} f_8(\tau) = 2E_4(\tau) \end{align}\]

という関係で結ばれる．

また，\(f_{12}(\tau)\) を

\[\begin{align} f_{12}(\tau) := \theta_2^4\theta_4^8+\theta_3^4\theta_4^8+\theta_4^4\theta_3^8 -\theta_2^4\theta_3^8-\theta_3^4\theta_2^8-\theta_4^4\theta_2^8 \end{align}\]

によって定義すると，

\[\begin{align} f_{12}(T\tau) = f_{12}(\tau),\hspace{12pt} f_{12}(S\tau) = \tau^6f_{12}(\tau) \end{align}\]

が成立する．定数項は \(2\) で，ウェイト \(6\) の保型形式は定数倍を除いてただ一つだから，

\[\begin{align} f_{12}(\tau) &= 2E_6(\tau) \end{align}\]

が成立する．

まとめると，エータ関数（の \(6\) 乗）とアイゼンシュタイン級数をテータ定数で表す方法として，

\[\begin{align} E_4 &= \frac{1}{2} \left(\theta_2^8 + \theta_3^8 + \theta_4^8\right),\\ E_6 &= \frac{1}{2} \left(\theta_2^4\theta_4^8+\theta_3^4\theta_4^8+\theta_4^4\theta_3^8 -\theta_2^4\theta_3^8-\theta_3^4\theta_2^8-\theta_4^4\theta_2^8\right),\\ \eta^6 &= \frac{1}{4}\theta_2^2\theta_3^3\theta_4^2 \end{align}\]

を得る．ただし省略した引数は全て \(\tau\)．ところで，テータ定数に関する \(4\) 次の関係式として，有名なヤコビの恒等式がある：

\[\begin{align} \theta_2^4-\theta_3^4+\theta_4^4=0 \end{align}\]

これを利用して \(\theta_2\) を消去しよう．

\[\begin{align} E_4 &= \theta_3^8-\theta_3^4\theta_4^4+\theta_4^8,\\ E_6 &= \frac{1}{2}\left(-2\theta_3^{12}+3\theta_3^8\theta_4^4+3\theta_3^4\theta_4^8-2\theta_4^{12}\right),\\ \eta^6 &= \frac{1}{4}\sqrt{\theta_3^4-\theta_4^4}\,\theta_3^2\theta_4^2 \end{align}\]

さらに，テータ定数について，「倍角公式」が

\[\begin{align} \theta_2(2\tau)^2 &= \frac{1}{2}\left(\theta_3(\tau)^2-\theta_4(\tau)^2\right),\\ \theta_3(2\tau)^2 &= \frac{1}{2}\left(\theta_3(\tau)^2+\theta_4(\tau)^2\right),\\ \theta_4(2\tau)^2 &= \theta_3(\tau)\theta_4(\tau),\\ \end{align}\]

「半角公式」が

\[\begin{align} \theta_2(\tau)^2 &= 2\theta_2(2\tau)\theta_3(2\tau),\\ \theta_3(\tau)^2 &= \theta_2(2\tau)^2+\theta_3(2\tau)^2,\\ \theta_4(\tau)^2 &= -\theta_2(2\tau)^2+\theta_3(2\tau)^2 \end{align}\]

の形で成り立つ．これを使うと，

\[\begin{align} E_4(\tau) &= \theta_3(2\tau)^8+14\,\theta_3(2\tau)^4\theta_2(2\tau)^4+\theta_2(2\tau)^8,\\ E_6(\tau) &= \theta_3(2\tau)^{12}-33\,\theta_3(2\tau)^8\theta_2(2\tau)^4-33\,\theta_3(2\tau)^4\theta_2(2\tau)^8+\theta_2(2\tau)^{12},\\ 2\eta(\tau)^6 &= \theta_3(2\tau)\theta_2(2\tau)\left(\theta_3(2\tau)^4-\theta_2(2\tau)^4\right) \end{align}\]

が導かれる．3つ目の式だけルートの取り方に不定性があるが，\(q-\)展開での主要項を比較すればよい．

\((1,\,14,\,1),\, (1,\,-33,\,-33,1)\) が現れた．こうして次の事実が分かる：基本正八面体多項式とエータ関数・アイゼンシュタイン級数との関係として，

\[\begin{align} V_8(\theta_3(2\tau), \theta_2(2\tau)) &= E_4(\tau),\\ V_{12}(\theta_3(2\tau), \theta_2(2\tau)) &= E_6(\tau),\\ V_6(\theta_3(2\tau), \theta_2(2\tau)) &= 2\,\eta(\tau)^6\\ \end{align}\]

が成立する．

Broué–Enguehard 写像 と重み枚挙多項式

このように \(2\) 変数斉次多項式に \(\theta_3(2\tau),\theta_2(2\tau)\) を対応させる写像は，線形符号理論の重み枚挙多項式(weight enumerator)に関連して Broué–Enguehard 写像 と呼ばれる［Bannai, p.244］．少々脱線にはなるが，重み枚挙多項式に見られる現象に関して概要として次の事実だけ述べておく（いずれ独立した記事は書く予定）．

\([8,4,4]\) 拡大ハミング符号 \(e_8\) の重み枚挙多項式 \(W_{e_8}(x,y)\) と 拡大ゴレイ符号 \(G_{24}\)の重み枚挙多項式 \(W_{G_{24}}(x,y)\) について，

\[\begin{align} W_{e_8}(x,y) &= x^8+7\cdot 2\,x^4y^4+y^8\\ &= V_{8}(x,y),\\ W_{G_{24}}(x,y) &= x^{24}+23\cdot 33\,x^{16}y^8+23\cdot 112\,x^{12}y^{12}+23\cdot 33\,x^8y^{16}+y^{24}\\ &= V_{8}(x,y)^3 - 42V_{6}(x,y)^4 \end{align}\]

である［Conway, 第7章］．重偶自己双対符号の重み枚挙多項式はこのふたつの多項式（Gleasonの定理）として表される．特に，長さ \(8n\) の極限的(extremal)重偶自己双対符号 \(C_{8n}\) の重み枚挙多項式 \(W_{C_{8n}}\) の最初のいくつかの例は，

\[\begin{align} W_{C_{16}}(x,y) =& x^{16} + 28 \, x^{12} y^{4} + 198 \, x^{8} y^{8} + 28 \, x^{4} y^{12} + y^{16},\\ W_{C_{32}}(x,y) =& x^{32} + 31\cdot20\, x^{24} y^{8} + 31\cdot448 \,x^{20} y^{12} + 31\cdot1178 \, x^{16} y^{16} + \cdots + y^{32},\\ W_{C_{40}}(x,y) =& x^{40} + 285 \, x^{32} y^{8} + 21280 \, x^{28} y^{12} + 239970 \, x^{24} y^{16} + 525504 \, x^{20} y^{20} + \cdots + y^{40},\\ W_{C_{48}}(x,y) =& x^{48} + 47\cdot368 \, x^{36} y^{12} + 47\cdot11385 \, x^{32} y^{16} + 47\cdot85008 \, x^{28} y^{20} \\ &+ 47\cdot163440 \, x^{24} y^{24} + \cdots +y^{48},\\ W_{C_{56}}(x,y) =& x^{56} + 8190 \, x^{44} y^{12} + 622314 \, x^{40} y^{16} + 11699688 \, x^{36} y^{20} + 64909845 \, x^{32} y^{24} \\ &+ 113955380 \, x^{28} y^{28} + \cdots + y^{56},\\ W_{C_{64}}(x,y) =&x^{64} + 2976 \, x^{52} y^{12} + 454956 \, x^{48} y^{16} + 18275616 \, x^{44} y^{20} + 233419584 \, x^{40} y^{24}\\ &+ 1041971008 \, x^{36} y^{28} + 1706719014 \, x^{32} y^{32} + \cdots + y^{64},\\ W_{C_{72}}(x,y) =& x^{72} + 71\cdot3519 \, x^{56} y^{16} + 71\cdot255024 \, x^{52} y^{20} + 71\cdot6520605 \, x^{48} y^{24} \\ &+ 71\cdot61934400 \, x^{44} y^{28} + 71\cdot233841069 \, x^{40} y^{32} + 71\cdot362770720 \, x^{36} y^{36} + \cdots + y^{72},\\ W_{C_{80}}(x,y) =&x^{80} + 79\cdot1235 \, x^{64} y^{16} + 79\cdot163072 \, x^{60} y^{20} + 79\cdot7469280 \, x^{56} y^{24} \\ &+ 79\cdot134027520 \, x^{52} y^{28} + 79\cdot1008957950 \, x^{48} y^{32} + 79\cdot3332958720 \, x^{44} y^{36} \\ &+ 79\cdot4950713152 \, x^{40} y^{40} + \cdots + y^{80} \end{align}\]

となっている．余談だが \(8n=72\) のケースは 「\([72,36,16]\) 重偶自己双対符号の存在性」という有名な未解決問題に関係している［Harada, A018236］．

見ての通り，\(8n-1\) が素数であるケース (\(n=1,3,4,6,9,10\)) では，中間項の係数が全て \(8n-1\) で割り切れている．

この中で少なくとも \(8n-1=7,23\)，つまり \([8,4,4]\) ハミング符号と拡大ゴレイ符号の場合には，組合せ論的な解釈がありうる．

前者の場合，位数 \(1344=7\cdot 192\) の群が8つの成分の入れ替えによって自己同型群として作用している．位数7の元が存在していて重みが1か7の符号語は存在しないから，重み0と8を除いて固定点はない．したがって，互いに重みが等しい符号語の数は0と8を除いて7の倍数になる．

後者の場合，自己同型群は位数 \(244823040=23\cdot 10644480\) の単純群である24次のマシュー群 \(M_{24}\) で，同様の議論が成立する．

一般に正多面体多項式の係数は全てが非負にはならないからそのまま何かの母関数とみなすことはできないが，何らかの組合せ論的な解釈があると嬉しいな，というのが今の気持ち．

レベル4の主合同部分群

話を戻そう．Broué–Enguehard写像による正八面体多項式と保型形式との結びつきは何を意味するのだろうか．

\[\begin{align} \alpha(\tau):=\theta_3(2\tau),\hspace{12pt} \beta(\tau):=\theta_2(2\tau) \end{align}\]

とする．\(SL(2,\mathbb{Z})\) の生成元 \(T,S\) の \(\tau\) への作用で\(\alpha(\tau),\,\beta(\tau)\) がどう変化するか見よう．

\[\begin{align} \alpha(T\tau) = \alpha(\tau),\hspace{12pt} \beta(T\tau) = i\beta(\tau) \end{align}\]

はすぐに分かる．\(S\)の作用は少しだけ厄介で，

\[\begin{align} \alpha(S\tau)^2 &=\frac{-i\tau}{2}\left(\alpha(\tau)+\beta(\tau)\right)^2 ,\\ \beta(S\tau)^2 &=\frac{-i\tau}{2}\left(\alpha(\tau)-\beta(\tau)\right)^2 \end{align}\]

までは倍角公式と半角公式を使って素直に変形できる．ルートの取り方でどちらの符号をとればよいかが微妙．純虚の \(\tau\) に対してはどのテータも正の実数かつ \(\theta_3(\tau)>\theta_2(\tau)\) が成り立つことから，

\[\begin{align} \alpha(S\tau) &= \sqrt{-i\tau}\, \frac{\alpha(\tau)+\beta(\tau)}{\sqrt{2}},\\ \beta(S\tau) &= \sqrt{-i\tau}\, \frac{\alpha(\tau)-\beta(\tau)}{\sqrt{2}},\\ \end{align}\]

であって，\(\sqrt{-i\tau}\) の実部が正になる方を取ると整合する．

まとめて行列を使って書くと，

\[\begin{align} \begin{pmatrix} \alpha(T\tau)\\ \beta(T\tau) \end{pmatrix} &= \begin{pmatrix} 1&0\\ 0&i \end{pmatrix} \begin{pmatrix} \alpha(\tau)\\ \beta(\tau) \end{pmatrix},\\ \begin{pmatrix} \alpha(S\tau)\\ \beta(S\tau) \end{pmatrix} &= \sqrt{\frac{-i\tau}{2}} \begin{pmatrix} 1&1\\ 1&-1 \end{pmatrix} \begin{pmatrix} \alpha(\tau)\\ \beta(\tau) \end{pmatrix},\\ &= \tau^{1/2}\frac{\varepsilon^{-1}}{\sqrt{2}} \begin{pmatrix} 1&1\\ 1&-1 \end{pmatrix} \begin{pmatrix} \alpha(\tau)\\ \beta(\tau) \end{pmatrix} \end{align}\]

となる．\(\sqrt{-i\tau}\) のファクターの存在によって，\(\alpha, \beta\) への作用で線形表現とはみなせないが，それに非常に近いものではある．いったん無視して行列部分だけ取り出してこれらによって生成される群

\[\begin{align} \left\langle \begin{pmatrix} 1 & 0\\ 0 & i \end{pmatrix},\, \frac{1-i}{2} \begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix} \right\rangle \end{align}\]

を考えると，これはShephard-Toddによるユニタリ鏡映群の分類でNo.8と呼ばれる位数96の群になる［Bannai, p.245］．

手っ取り早くファクターの影響を消すには比を取って一次分数変換を考えればよく，

\[\begin{align} \chi(\tau) := \frac{\alpha(\tau)}{\beta(\tau)} \end{align}\]

とすると，

\[\begin{align} \chi(T^{-1}\tau)=i\chi(\tau),\hspace{12pt}\chi(S^{-1}\tau)=\frac{\chi(\tau)+1}{\chi(\tau)-1} \end{align}\]

から，

\[\begin{align} \psi: PSL(2,\mathbb{Z}) &\rightarrow PSL(2,\mathbb{C})\\ \psi(T) &= z \mapsto iz,\\ \psi(S) &= z\mapsto\frac{z+1}{z-1} \end{align}\]

という群準同型が生じる．値域は

\[\begin{align} \widetilde{O} = \left\langle \begin{pmatrix} \varepsilon & 0\\ 0 & \varepsilon^{-1} \end{pmatrix},\, \frac{1}{\sqrt{2}} \begin{pmatrix} i & i\\ i & -i \end{pmatrix} \right\rangle \subset SU(2) \end{align}\]

による一次分数変換の全体で，正八面体群 \(\cong\) 4次対称群に同型になる．\(\widetilde{O}\) は位数48の二項正八面体群である．

\(\psi\) の核はレベル4の主合同部分群の中心による剰余群 \(\overline{\Gamma(4)}\) で，実は \(\alpha(\tau), \beta(\tau)\) は \(\Gamma(4)\) に関するウェイト \(1/2\) の保型形式になっている．このことを踏まえると，Broué–Enguehar写像は \(PSL(2,\mathbb{Z})/\overline{\Gamma(4)}\) の相対不変式へ，\(SL(2,\mathbb{Z})\) 全体ではなく \(\Gamma(4)\) に関する保型性までしか持たない関数を代入してフルの保型性を回復する方法だと見ることができる．

正八面体のケースは古典的なモジュラーラムダ関数との関わり，係数に現れる素数など調べるべきことがまだまだたくさんある．が，ここで一旦切り上げて，再び正二十面体について考えよう．

正二十面体群の場合

正二十面体方程式

正二十面体では，頂点・面・辺に対応して次の3つが基本正二十面体多項式になるのだった（過去記事）．

\[\begin{align} V_{12}(x,y)&=x^{11}y+11x^6y^6-xy^{11},\\ V_{20}(x,y)&= x^{20}-228x^{15}y^5+494x^{10}y^{10}+228x^5y^{15}+y^{20},\\ V_{30}(x,y)&=x^{30}+522x^{25}y^5-10005x^{20}y^{10}-10005x^{10}y^{20}-522x^5y^{25}+y^{30} \end{align}\]

そしてこれらの間には

\[\begin{align} V_{20}(x,y)^3-V_{30}(x,y)^2 = 1728\left(-V_{12}(x,y)\right)^5 \end{align}\]

という関係が成り立つ．Broué–Enguehard 写像に相当するものをこの場合でも考えられるはずだ．\(x,\,y\) には何を代入すればよいだろうか？

答えはクラインの「正二十面体本」にほとんど書かれている．

クラインの関心は，正二十面体の対称性を五次方程式の求解に利用することだった．「正二十面体本」は正式には “Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade“（『正二十面体と五次方程式の解法講義』）で、邦訳が『正20面体と5次方程式』のタイトルで出ている［Klein1］。

ここで重要な役割を果たすのが，「正二十面体方程式」と呼ばれる60次の補助方程式である．クラインは，一般の5次方程式を

• チルンハウス変換によって \(3,\,4\) 次の項がない標準形に変換する．
• 更に変数変換して「解の偶置換」（5次交代群）と「正二十面体の回転」（正二十面体群）との同型写像を与える．

という手順によって正二十面体方程式に帰着した［Klein1, Nash, Hashimoto2］．一見次数が上がってより難しくなっているようにも思われるが，これには良い性質があるのだ．

正二十面体方程式は \(Z\) をパラメーターに持つ \(t\) に関する方程式で，次の形をしている：

\[\begin{align} V_{20}(t,1)^3+1728ZV_{12}(t,1)^5=0. \end{align}\]

あえて具体的に書くなら，

\[\begin{align} (t^{20}-228\,t^{15}+494\,t^{10}+228\,t^5+1)^3 + 1728Z(t^{11}+11\,t^6-t)^5 = 0. \end{align}\]

変形すると，

\[\begin{align} \frac{V_{20}(t,1)^3}{1728(-V_{12}(t,1))^5} = Z. \end{align}\]

もし期待するように基本正二十面体多項式たちとモジュラー形式との間に対応関係――\(t\) を \(\tau\) で表す――が存在すれば，

\[\begin{align} \frac{j(\tau)}{1728}=\frac{E_4(\tau)^3}{1728\Delta(\tau)}=Z \end{align}\]

が成立する．ただし，\(j(\tau)\) はクラインの \(j-\)関数で，

\[\begin{align} j(\tau) = \frac{E_4(\tau)^3}{\Delta(\tau)} = \frac{1728E_4(\tau)^3}{E_4(\tau)^3-E_6(\tau)^2}. \end{align}\]

したがって，

\[\begin{align} j(\tau) = 1728Z \end{align}\]

を \(\tau\) について解くことができれば，\(t\) に代入することで正二十面体方程式が解けることになる．実際これを解くことはできて，解は超幾何級数によって与えられることが知られている．

クラインが \(t\) と \(\tau\) の間に見出したのは次の関係だった［Klein1 p.141］：

\[\begin{align} t = q^{1/5}\frac{\sum_{n\in\mathbb{Z}}(-1)^nq^{(5n^2-3n)/2}}{\sum_{n\in\mathbb{Z}}(-1)^nq^{(5n^2-n)/2}}=:\Lambda(\tau) \end{align}\]

これが \(\tau\) による \(t\) のパラメトライズだ．

ロジャース・ラマヌジャン恒等式

ここで唐突だがヤコビの三重積公式と見比べる．

\[\begin{align} \sum_{n\in\mathbb{Z}}z^n q^{(n^2+n)/2} = \prod_{n=1}^\infty (1-q^n)(1+zq^n)(1+z^{-1}q^{n-1}). \end{align}\]

\(z\rightarrow -q^{-4},\,q\rightarrow q^{5}\) と置き換えてみると，

\[\begin{align} \sum_{n\in\mathbb{Z}} (-1)^n q^{(5n^2-3n)/2} &= \prod_{n=1}^\infty (1-q^{5n})(1-q^{5n-4})(1-q^{5n-1})\\ &= \prod_{n=1}^\infty \frac{(1-q^{5n-4})(1-q^{5n-3})(1-q^{5n-2})(1-q^{5n-1})(1-q^{5n})}{(1-q^{5n-3})(1-q^{5n-2})}\\ &=q^{-1/24}\eta(\tau) \prod_{n=1}^{\infty}\frac{1}{(1-q^{5n-3})(1-q^{5n-2})}. \end{align}\]

同様に，

\[\begin{align} \sum_{n\in\mathbb{Z}} (-1)^n q^{(5n^2-n)/2} =q^{-1/24}\eta(\tau) \prod_{n=1}^{\infty}\frac{1}{(1-q^{5n-4})(1-q^{5n-1})}. \end{align}\]

したがって，

\[\begin{align} G(q):=\prod_{n=1}^\infty \frac{1}{(1-q^{5n-4})(1-q^{5n-1})},\\ H(q):=\prod_{n=1}^\infty \frac{1}{(1-q^{5n-3})(1-q^{5n-2})},\\ \end{align}\]

と定義すると，

\[\begin{align} R(q) &:= q^{1/5}\frac{H(q)}{G(q)} = \Lambda(\tau) \end{align}\]

である．平方剰余に関するルジャンドルの記号を使うと，

\[\begin{align} \Lambda(\tau) = q^{1/5}\prod_{n=1}^\infty\frac{(1-q^{5n-4})(1-q^{5n-1})}{(1-q^{5n-3})(1-q^{5n-2})} = q^{1/5} \prod_{n=1}^\infty 1-q^{(\frac{n}{5})} \end{align}\]

とも書ける． なぜこんなふうに \(G(q), H(q)\) を使って表したかというと， この2つが有名なロジャース・ラマヌジャン恒等式の登場人物だからである．それぞれ「第一恒等式」と「第二恒等式」が以下で与えられる［Andrews1第4章, Yamada1第6講］：

\[\begin{align} G(q) &= \prod_{n=1}^\infty \frac{1}{(1-q^{5n-4})(1-q^{5n-1})} =1+\sum_{n=1}^\infty\frac{q^{n^2}}{(1-q)(1-q^2)\cdots(1-q^n)},\\ H(q) &= \prod_{n=1}^\infty \frac{1}{(1-q^{5n-3})(1-q^{5n-2})} =1+\sum_{n=1}^\infty\frac{q^{n^2+n}}{(1-q)(1-q^2)\cdots(1-q^n)} \end{align}\]

それぞれ右側の等号は，両側を母関数だと思うと，第一恒等式について，

全ての非負整数に対して，

「法 \(5\) で \(\pm 1\) となる非負整数へ分割する方法の総数」(分割G-I)

\(=\) 「どの \(2\) 数をとっても差が \(2\) 以上となる非負整数へ分割する方法の総数」(分割G-II)

となることを，第二恒等式について， 全ての非負整数に対して，

「法 \(5\) で \(\pm 2\) となる非負整数へ分割する方法の総数」(分割H-I)

\(=\) 「どの \(2\) 数をとっても差が \(2\) 以上となる \(2\) 以上の整数へ分割する方法の総数」(分割H-II)

という解釈ができる．

たとえば \(n=11\) の分割に対して，

\[\begin{align} \begin{array}{|l|l|} \hline {\rm G-I} & {\rm G-II} \\ \hline 1+1+1+1+1+1+1+1+1+1+1 & 1+4+6 \\ 1+1+1+1+1+1+1+4 & 1+3+7 \\ 1+1+1+4+4 & 4+7 \\ 1+1+1+1+1+6 & 3+8 \\ 1+4+6 & 2+9 \\ 1+1+9 & 1+10 \\ 11 & 11 \\ \hline \end{array} \end{align}\] \[\begin{align} \begin{array}{|l|l|} \hline {\rm H-I} & {\rm H-II} \\ \hline 2+2+2+2+3 & 4+7\\ 2+3+3+3 & 3+8\\ 2+2+7 & 2+9\\ 3+8 & 11\\ \hline \end{array} \end{align}\]

Table 3. 制約付きの \(11\) の分割．

というふうに，IとII，\(2\) 種類の分割がGとHのそれぞれで同数になっていることが分かる．実際に展開すると，

\[\begin{align} G(q) &= 1+q+q^2+q^3+2\,q^4+2\,q^5+3\,q^6+3\,q^7+4\,q^8+5\,q^9+6\,q^{10}+7\,q^{11}+O(q^{12}),\\ H(q) &= 1+q^2+q^3+q^4+q^5+2\,q^6+2\,q^7+3\,q^8+3\,q^9+4\,q^{10}+4\,q^{11}+O(q^{12}) \end{align}\]

と，\(q^{11}\) の項の係数は \(G(q)\) が \(7\)，\(H(q)\) が \(4\) で，表に現れた分割の個数と一致する．

また，\(R(q)\) は次の連分数展開を持つ［Yamada1 p.61］：

\[\begin{align} R(q) = \cfrac{q^{1/5}}{1+ \cfrac{q}{1+\cfrac{q^2}{1+\cfrac{q^3}{1+\ddots}}} }. \end{align}\]

\(q=1\) の場合に

\[\begin{align} R(1)^{-1} = \frac{1+\sqrt{5}}{2} \end{align}\]

と黄金比が現れることは（収束性については大雑把に扱えば）簡単に示せる．

ラマヌジャンはたくさんの特殊値を求めていて，ハーディを驚愕させたという彼の手紙の中に

\[\begin{align} R(e^{-2\pi}) = \sqrt{\frac{5+\sqrt{5}}{2}}-\frac{1+\sqrt{5}}{2} \end{align}\]

という等式が含まれていたことは有名な話である［Takase］．この等式は後で再び登場する．

正二十面体と保型形式

話を戻すと，少なくともクラインは

\[\begin{align} \frac{V_{20}(\Lambda(\tau), 1)^3}{(-V_{12}(\Lambda(\tau),1))^5} = j(\tau)=\frac{E_4(\tau)^3}{\Delta(\tau)} \end{align}\]

を正二十面体本の中に書いていることになる．

これは，共通の関数 \(c(\tau)\) が存在して，

\[\begin{align} V_{20}\left(q^{1/5}H(q), G(q)\right) &= c(q) E_4(\tau)^3,\\ -V_{12}\left(q^{1/5}H(q), G(q)\right)^5 &= c(q) \Delta(\tau) \end{align}\]

となることを意味する．

一方，ラマヌジャンは “Algebraic relations between certain infinite products” と題する論文［Ramanujan1］の中で

\[\begin{align} H(q)G^{11}(q) - q^2G(q)H^{11}(q) = 1+11q\,G^6(q)H^6(q) \end{align}\]

を，また，同値な等式として

\[\begin{align} \frac{1}{R^5(q)} - 11 -R^5(q) = \left(\frac{\eta(\tau)}{\eta(5\tau)}\right)^6 \end{align}\]

を与えている［Andrews2 p.61］．これは

\[\begin{align} g(\tau) &:= q^{-1/60}G(q),\\ h(\tau) &:= q^{11/60}H(q) \end{align}\]

とすると，

\[\begin{align} h(\tau)^{11} g(\tau) + 11 h(\tau)^6g(\tau)^6 -h(\tau)g(\tau)^{11} &=-1 \end{align}\]

となることを意味する．さらにエータ関数を適当にかけて

\[\begin{align} \phi_1(\tau) &:= \eta(\tau)^{2/5} h(\tau),\\ \phi_2(\tau) &:= \eta(\tau)^{2/5} g(\tau),\\ \end{align}\]

を定義すると（上が \(h\) で下が \(g\) になっていることに注意），

\[\begin{align} V_{12}(\phi_1(\tau), \phi_2(\tau)) &= -\eta(\tau)^{24/5} \end{align}\]

を得る．望んでいた関係式が現れた．これがいわば正二十面体版のBroué–Enguehard写像だ．これを使うと，

\[\begin{align} V_{20}(\phi_1(\tau), \phi_2(\tau)) &= E_4(\tau),\\ V_{30}(\phi_1(\tau), \phi_2(\tau)) &= E_6(\tau) \end{align}\]

も同様に成り立つ．

ほんとうだろうか．

ちょっと計算してみる．

\(G(q), H(q)\) の係数は既に見た。エータ関数の \(2/5\) 乗は，

\[\begin{align} \eta(q)^{2/5} =q^{1/60}\left( 1-\frac{2\,q}{5}-\frac{13\,q^2}{25} -\frac{38\,q^3}{125}-\frac{221\,q^4}{625} +\frac{182\,q^5}{15625} + O(q^6)\right) \end{align}\]

だから，

\[\begin{align} \phi_1(\tau) &= q^{1/5} \left(1-\frac{2 q}{5}+\frac{12 {q^{2}}}{25}+\frac{37 {q^{3}}}{125}-\frac{171 {q^{4}}}{625}-\frac{3318 {q^{5}}}{15625}+O(q^6)\right),\\ \phi_2(\tau) &= 1+\frac{3 q}{5}+\frac{2 {q^{2}}}{25}-\frac{28 {q^{3}}}{125}+\frac{264 {q^{4}}}{625}+\frac{532 {q^{5}}}{15625}+O(q^6) \end{align}\]

と展開される．思い切って

\[\begin{align} \phi_1(\tau) &\simeq q^{1/5},\\ \phi_2(\tau) &\simeq 1+\frac{3\,q}{5} \end{align}\]

までで打ち切ると，

\[\begin{align} \phi_1(\tau)^5 & \simeq q,\\ \phi_2(\tau)^5 & \simeq 1+3\,q \end{align}\] \[\begin{align} V_{20}(\phi_1(\tau),\phi_2(\tau)) &\simeq (1+3\,q)^4 + 228\, q(1+3\,q)^3\\ &\simeq 1+240\,q,\\ V_{30}(\phi_1(\tau),\phi_2(\tau)) &\simeq (1+3\,q)^6-522\,q(1+3\,q)^5\\ &\simeq 1-504\,q \end{align}\]

とアイゼンシュタイン級数のリーディングタームが現れる．証明にはなっていないが，ただのテイラー展開なので，数式処理ソフトを使えば簡単にいくらでも高次の項まで一致することを確かめることができる．

さて，\(\phi_1, \phi_2\) が \(SL(2,\mathbb{Z})\) の生成元による作用でどう変化するか見よう． \(T:\tau\mapsto \tau+1\) に対して，

\[\begin{align} \phi_1(T\tau) &= \zeta \phi_1(\tau),\\ \phi_2(T\tau) &= \phi_2(\tau),\\ \end{align}\]

は易しい．

\(S:\tau\mapsto -1/\tau\) のほうはやはり少し複雑になる．

まず，

\[\begin{align} \phi_1(\tau) &= \eta(\tau)^{2/5}q^{11/60}\cdot q^{1/24}\eta(\tau)^{-1}\sum_{n\in \mathbb{Z}}(-1)^nq^{(5n^2-3n)/2}\\ &= q^{9/40} \eta(\tau)^{-3/5} \sum_{n\in \mathbb{Z}}(-1)^nq^{(5n^2+3n)/2},\\ \phi_2(\tau) &= \eta(\tau)^{2/5}q^{-1/60}\cdot q^{1/24}\eta(\tau)^{-1}\sum_{n\in \mathbb{Z}}(-1)^nq^{(5n^2-n)/2}\\ &= q^{1/40} \eta(\tau)^{-3/5} \sum_{n\in \mathbb{Z}}(-1)^nq^{(5n^2+n)/2},\\ \end{align}\]

という形にする．

先に登場したテータ「定数」はテータ「関数」に \(u=0\) を代入したものであって，2変数関数であるテータ関数は

\[\begin{align} \theta_1(u, \tau) &= -i \sum_{n\in \mathbb{Z}} (-1)^nq^{(n+1/2)^2/2} z^{n+1/2},\\ \theta_2(u,\tau) &= \sum_{n\in\mathbb{Z}} q^{(n+1/2)^2/2} z^{n+1/2},\\ \theta_3(u,\tau) &= \sum_{n\in\mathbb{Z}} q^{n^2/2} z^n,\\ \theta_4(u,\tau) &= \sum_{n\in\mathbb{Z}} (-1)^n q^{n^2/2} z^n \end{align}\]

と定義される．ただし \(z=\mathbf{e}(u)\)．じっと見ると，

\[\begin{align} \sum_{n\in \mathbb{Z}}(-1)^nq^{(5n^2+3n)/2} &= \theta_4\left(\frac{3\tau}{2}, 5\tau\right),\\ \sum_{n\in \mathbb{Z}}(-1)^nq^{(5n^2+n)/2} &= \theta_4\left(\frac{\tau}{2}, 5\tau\right),\\ \end{align}\]

と表せることが分かる（本質的にはテータ関数はひとつなので実はどれを使っても似た結果は得られるがここでは \(\theta_4\) を選ぶ）．つまり，

\[\begin{align} \phi_1(\tau) &= q^{9/40} \eta(\tau)^{-3/5} \theta_4\left(\frac{3\tau}{2}, 5\tau\right),\\ \phi_2(\tau) &= q^{1/40} \eta(\tau)^{-3/5} \theta_4\left(\frac{\tau}{2}, 5\tau\right).\\ \end{align}\]

テータ定数の変換公式は既に見たが，より一般的なテータ関数の変換公式として

\[\begin{align} \theta_1\left(\frac{u}{\tau}, \frac{-1}{\tau}\right)&=-i\sqrt{-i\tau}\, \mathbf{e}\left(\frac{u^2}{2\tau}\right)\theta_1(u,\tau),\\ \theta_2\left(\frac{u}{\tau}, \frac{-1}{\tau}\right)&=\sqrt{-i\tau}\,\, \mathbf{e}\left(\frac{u^2}{2\tau}\right)\theta_4(u,\tau),\\ \theta_3\left(\frac{u}{\tau}, \frac{-1}{\tau}\right)&=\sqrt{-i\tau}\, \mathbf{e}\left(\frac{u^2}{2\tau}\right)\theta_3(u,\tau),\\ \theta_4\left(\frac{u}{\tau}, \frac{-1}{\tau}\right)&=\sqrt{-i\tau}\, \mathbf{e}\left(\frac{u^2}{2\tau}\right)\theta_2(u,\tau),\\ \end{align}\]

が知られている．第4の等式に \((u,\tau)\rightarrow(-3/10, \tau/5),\,(-1/10, \tau/5)\) を代入して，

\[\begin{align} \theta_4\left(\frac{-3}{2\tau}, \frac{-5}{\tau}\right) &= \sqrt{\frac{-i\tau}{5}}\,\mathbf{e}\left(\frac{9}{40\tau}\right)\theta_2\left(\frac{-3}{10},\,\frac{\tau}{5}\right),\\ \theta_4\left(\frac{-1}{2\tau}, \frac{-5}{\tau}\right) &= \sqrt{\frac{-i\tau}{5}}\,\mathbf{e}\left(\frac{1}{40\tau}\right)\theta_2\left(\frac{-1}{10},\,\frac{\tau}{5}\right). \end{align}\]

右辺を \(\theta_4\) に戻したい．\(\theta_2\) の \(q-\)展開は

\[\begin{align} \theta_2(u,\tau) &=\sum_{n\in\mathbb{Z}} q^{(n+1/2)^2/2} z^{n+1/2},\\ &=\sum_{n\in\mathbb{Z}} \mathbf{e}\left(\frac{(2n+1)^2\tau}{8} + \frac{(2n+1)u}{2}\right) \end{align}\]

だから，

\[\begin{align} \theta_2\left(\frac{-3}{10},\frac{\tau}{5}\right) =&\sum_{n\in\mathbb{Z}} \mathbf{e}\left(\frac{(2\,n+1)^2\tau}{40} + \frac{-3\,(2\,n+1)}{20}\right)\\ =&\sum_{n\in \mathbb{Z}} \mathbf{e}\left(\frac{(10\,n+1)^2\tau}{40} + \frac{-3\,(10\,n+1)}{20}\right)&&n\rightarrow 5n\\ &+\sum_{n\in \mathbb{Z}} \mathbf{e}\left(\frac{(10\,n+3)^2\tau}{40} + \frac{-3\,(10\,n+3)}{20}\right)&&n\rightarrow 5n+1\\ &+\sum_{n\in \mathbb{Z}} \mathbf{e}\left(\frac{(10\,n+5)^2\tau}{40} + \frac{-3\,(10\,n+5)}{20}\right)&&n\rightarrow 5n+2\\ &+\sum_{n\in \mathbb{Z}} \mathbf{e}\left(\frac{(-10\,n-3)^2\tau}{40} + \frac{-3\,(-10\,n-3)}{20}\right)&&n\rightarrow -5n-2\\ &+\sum_{n\in \mathbb{Z}} \mathbf{e}\left(\frac{(-10\,n-1)^2\tau}{40} + \frac{-3\,(-10\,n-1)}{20}\right)&&n\rightarrow -5n-1\\ =& q^{1/40}\mathbf{e}\left(\frac{-3}{20}\right) \sum_{n\in \mathbb{Z}} (-1)^n q^{(5n^2+n)/2}\\ &+q^{9/40}\mathbf{e}\left(\frac{-9}{20}\right)\sum_{n\in \mathbb{Z}} (-1)^n q^{(5n^2+3n)/2}\\ &+0\\ &+q^{9/40}\mathbf{e}\left(\frac{9}{20}\right)\sum_{n\in \mathbb{Z}} (-1)^n q^{(5n^2+3n)/2}\\ &+q^{1/40}\mathbf{e}\left(\frac{3}{20}\right)\sum_{n\in \mathbb{Z}} (-1)^n q^{(5n^2+n)/2}\\ =& \left(\mathbf{e}\left(\frac{3}{20}\right)+\mathbf{e}\left(\frac{-3}{20}\right) \right)q^{1/40} \theta_4\left(\frac{\tau}{2},5\tau\right)\\ &+\left(\mathbf{e}\left(\frac{9}{20}\right)+\mathbf{e}\left(\frac{-9}{20}\right) \right)q^{9/40} \theta_4\left(\frac{3\tau}{2},5\tau\right) \end{align}\]

とすれば \(\theta_4\) に戻すことができる．\(5\) に関する剰余でまとめるのがみそだ．同様に，

\[\begin{align} \theta_2\left(\frac{-1}{10},\frac{\tau}{5}\right) =& \left(\mathbf{e}\left(\frac{1}{20}\right)+\mathbf{e}\left(\frac{-1}{20}\right) \right)q^{1/40} \theta_4\left(\frac{\tau}{2},5\tau\right)\\ &+\left(\mathbf{e}\left(\frac{3}{20}\right)+\mathbf{e}\left(\frac{-3}{20}\right) \right)q^{9/40} \theta_4\left(\frac{3\tau}{2},5\tau\right). \end{align}\]

まとめると，

\[\begin{align} \mathbf{e}\left(\frac{-9}{40\tau}\right) \theta_4\left( \frac{-3}{2\tau},\frac{-5}{\tau} \right) =\sqrt{\frac{-i\tau}{5}} \Bigg\lbrack&\left(\mathbf{e}\left(\frac{3}{20}\right)+\mathbf{e}\left(\frac{-3}{20}\right) \right)q^{1/40} \theta_4\left(\frac{\tau}{2},5\tau\right)\\ &+\left(\mathbf{e}\left(\frac{9}{20}\right)+\mathbf{e}\left(\frac{-9}{20}\right) \right)q^{9/40} \theta_4\left(\frac{3\tau}{2},5\tau\right)\Bigg\rbrack ,\\ \mathbf{e}\left(\frac{-1}{40\tau}\right) \theta_4\left( \frac{-1}{2\tau},\frac{-5}{\tau} \right) =\sqrt{\frac{-i\tau}{5}} \Bigg\lbrack&\left(\mathbf{e}\left(\frac{1}{20}\right)+\mathbf{e}\left(\frac{-1}{20}\right) \right)q^{1/40} \theta_4\left(\frac{\tau}{2},5\tau\right)\\ &+\left(\mathbf{e}\left(\frac{3}{20}\right)+\mathbf{e}\left(\frac{-3}{20}\right) \right)q^{9/40} \theta_4\left(\frac{3\tau}{2},5\tau\right)\Bigg\rbrack . \end{align}\]

さらに，エータ関数の変換性は

\[\begin{align} \eta\left(\frac{-1}{\tau}\right) = \sqrt{-i\tau}\,\eta(\tau)=\mathbf{e}\left(-\frac{1}{8}\right)\tau^{1/2}\,\eta(\tau) \end{align}\]

だから，この \((-3/5)\) 乗を先の式の両辺に乗じることで，

\[\begin{align} \mathbf{e}\left(\frac{-9}{40\tau}\right) \eta\left(\frac{-1}{\tau}\right)^{-3/5}&\theta_4\left( \frac{-3}{2\tau},\frac{-5}{\tau} \right)\\ &=\frac{\tau^{1/5}}{\sqrt{5}}\eta(\tau)^{-3/5} \Bigg\lbrack\left(\mathbf{e}\left(\frac{1}{10}\right)+\mathbf{e}\left(\frac{-1}{5}\right) \right)q^{1/40} \theta_4\left(\frac{\tau}{2},5\tau\right)\\ &\hspace{80pt}+\left(\mathbf{e}\left(\frac{2}{5}\right)+\mathbf{e}\left(\frac{-1}{2}\right) \right)q^{9/40} \theta_4\left(\frac{3\tau}{2},5\tau \right)\Bigg\rbrack ,\\ \mathbf{e}\left(\frac{-1}{40\tau}\right) \eta\left(\frac{-1}{\tau}\right)^{-3/5}&\theta_4\left( \frac{-1}{2\tau},\frac{-5}{\tau} \right)\\ & =\frac{\tau^{1/5}}{\sqrt{5}}\eta(\tau)^{-3/5} \Bigg\lbrack\left(1+\mathbf{e}\left(\frac{-1}{10}\right) \right)q^{1/40} \theta_4\left(\frac{\tau}{2},5\tau\right)\\ &\hspace{80pt}+\left(\mathbf{e}\left(\frac{1}{10}\right)+\mathbf{e}\left(\frac{-1}{5}\right) \right)q^{9/40} \theta_4\left(\frac{3\tau}{2},5\tau\right)\Bigg\rbrack . \end{align}\]

よって，

\[\begin{align} \phi_1(S\tau) &= \frac{\tau^{1/5}}{\sqrt{5}}\left\lbrack(\zeta^2-1)\phi_1(\tau) + (-\zeta^3+\zeta^4)\phi_2(\tau)\right\rbrack\\ &= \frac{\zeta \tau^{1/5}}{\sqrt{5}}\left\lbrack(\zeta-\zeta^4)\phi_1(\tau) - (\zeta^2-\zeta^3)\phi_2(\tau)\right\rbrack,\\ \phi_2(S\tau) &= \frac{\tau^{1/5}}{\sqrt{5}}\left\lbrack(-\zeta^3+\zeta^4)\phi_1(\tau) + (1-\zeta^2)\phi_2(\tau)\right\rbrack\\ &= \frac{\zeta\tau^{1/5}}{\sqrt{5}}\left\lbrack-(\zeta^2-\zeta^3)\phi_1(\tau) - (\zeta-\zeta^4)\phi_2(\tau)\right\rbrack \end{align}\]

を得る．\(\phi_1(\tau), \phi_2(\tau)\) は虚軸上で実数値を取るから，\(\tau=ir^5\) (\(r\) は実数) のとき，\(\tau^{1/5}=r\zeta i\) となるように選ばなくてはならない．明らかにもう少し精密な議論が必要ではあるが，これを考慮して

\[\begin{align} \phi_1(S\tau) &= (-i\tau)^{1/5}\left( \frac{-(\zeta-\zeta^4)}{i\sqrt{5}}\phi_1(\tau) + \frac{\zeta^2-\zeta^3}{i\sqrt{5}}\phi_2(\tau)\right ),\\ \phi_2(S\tau) &= (-i\tau)^{1/5}\left(\frac{\zeta^2-\zeta^3}{i\sqrt{5}}\phi_1(\tau) + \frac{\zeta-\zeta^4}{i\sqrt{5}}\phi_2(\tau)\right). \end{align}\]

と書く．行列を使うと，

\[\begin{align} \begin{pmatrix} \phi_1(S\tau)\\ \phi_2(S\tau) \end{pmatrix} = (-i\tau)^{1/5} \begin{pmatrix} -\mu & \nu\\ \nu & \mu \end{pmatrix} \begin{pmatrix} \phi_1(\tau)\\ \phi_2(\tau) \end{pmatrix}. \end{align}\]

ただし，

\[\begin{align} \mu &= \frac{\zeta-\zeta^4}{i\sqrt{5}} = \frac{2}{\sqrt{5}}\sin\frac{2\pi}{5} =\sqrt{\frac{5+\sqrt{5}}{10}} \simeq 0.8506508083520399 =: \tilde{\mu},\\ \nu &= \frac{\zeta^2-\zeta^3}{i\sqrt{5}} = \frac{2}{\sqrt{5}}\sin\frac{4\pi}{5} =\sqrt{\frac{5-\sqrt{5}}{10}} \simeq 0.5257311121191337 =: \tilde{\nu}. \end{align}\]

……本当だろうか．

\(\tau=i\) での値で検証してみる．精度保証も収束性の考慮も何もない浮動小数点数による粗雑な計算だが，定義通りに無限乗積展開を利用すると，

\[\begin{align} \phi_1(i) &\simeq 0.28439742348932373 =: \tilde{x} ,\\ \phi_2(i) &\simeq 1.0011207431727707 =:\tilde{y} \end{align}\]

が分かる．この値を利用すると，

\[\begin{align} \left|\tilde{x}-(-\tilde{\mu}\tilde{x} + \tilde{\nu}\tilde{y})\right| < 10^{-16},\\ \left|\tilde{y}-(\tilde{\nu}\tilde{x} + \tilde{\mu}\tilde{y})\right| < 10^{-16},\\ \end{align}\]

が分かる．どうやら正しそうだ．

ラマヌジャンの連分数の特殊値

ところで，\(\phi_1(i),\,\phi_2(i)\) の数値計算による近似値の比を取ると

\[\begin{align} \frac{\phi_1(i)}{\phi_2(i)} \simeq \frac{\tilde{x}}{\tilde{y}}=\underline{0.284079043840412}38\cdots \end{align}\]

である．一方，

\[\begin{align} \sqrt{\frac{5+\sqrt{5}}{2}}-\frac{1+\sqrt{5}}{2} \simeq \underline{0.284079043840412}29\cdots . \end{align}\]

これは先ほど現れたラマヌジャンの連分数の値だ．

\[\begin{align} R(e^{-2\pi}) = \frac{\phi_1(i)}{\phi_2(i)}. \end{align}\]

\(R\) と \(\phi_1,\,\phi_2\) との関係は定義から従う（\(\tau=i\) で \(q=\exp(-2\pi)\)）が，\(\sqrt{(5+\sqrt{5})/2}-(1+\sqrt{5})/2\) という値はどこから出てくるのか．ここでは微妙に異なる二つの見方を与えよう．

一つ目はシンプルな固有ベクトルの計算だ． \(S\) に関する変換式から，

\[\begin{align} \begin{pmatrix} \phi_1(i)\\ \phi_2(i) \end{pmatrix} = \begin{pmatrix} -\mu & \nu\\ \nu & \mu \end{pmatrix} \begin{pmatrix} \phi_1(i)\\ \phi_2(i) \end{pmatrix}. \end{align}\]

だから，この行列の固有値1の固有ベクトルから値が決まる．

\[\begin{align} \begin{pmatrix} -\mu & \nu\\ \nu & \mu \end{pmatrix} = \begin{pmatrix} -\cos\theta & \sin\theta \\ \sin\theta & \cos\theta \end{pmatrix},\hspace{10pt} 0<\theta<\frac{\pi}{2} \end{align}\]

とすると，固有値1の固有ベクトルは \((\sin(\theta/2), \cos(\theta/2))^T\) である．したがって，

\[\begin{align} \frac{\phi_1(i)}{\phi_2(i)} = \frac{\sin(\theta/2)}{\cos(\theta/2)} =\frac{1-\cos\theta}{\sin\theta} =\frac{1}{\nu}-\frac{\mu}{\nu} =\sqrt{\frac{5+\sqrt{5}}{2}} - \frac{1+\sqrt{5}}{2} \end{align}\]

と定まる．

二つ目の見方でもやはり不動点を考えるが，正二十面体を通して幾何学的な意味が与えられる．同じ \(\theta\) を使って

\[\begin{align} U = i\begin{pmatrix} -\cos\theta & \sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \end{align}\]

としよう．行列式 \(1\) でユニタリだから \(U\in SU(2)\) である．パウリ行列を

\[\begin{align} \sigma_1=\begin{pmatrix} 0&1\\ 1&0 \end{pmatrix},\hspace{10pt} \sigma_2=\begin{pmatrix} 0&-i\\ i&0 \end{pmatrix},\hspace{10pt} \sigma_3&=\begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix} \end{align}\]

として四元数の虚部の基底を

\[\begin{align} \mathbf{i} = i\,\sigma_1,\hspace{10pt} \mathbf{j} = i\,\sigma_2,\hspace{10pt} \mathbf{k} = -i\,\sigma_3 \end{align}\]

にとる（詳細は割愛するがこの取り方は南極からの立体射影を採用しているため）と

\[\begin{align} U = \sin\theta\,\mathbf{i} + 0\,\mathbf{j} + \cos\theta\,\mathbf{k} \end{align}\]

だから，これは原点 \(O\) と単位球面上の点 \(P=(\sin\theta, 0, \cos\theta)\) を通る直線を軸とする \(\mathbb{R}^3\) の \(180^\circ\) 回転とみなせる．この \(P\) は何かというと，単位球面に内接する正二十面体が \(V_1=(0,0,1)\) と \(V_2=(\sin2\theta, 0, \cos2\theta)\) に頂点を持っていて辺 \(V_1V_2\) の中点が \(M\) であるとき，原点から単位球面への \(M\) の射影である．\(\angle V_1OV_2=2\theta\) について \(\cos 2\theta = 1/\sqrt{5},\, \sin2\theta=2/\sqrt{5}\) は正二十面体の性質から従って，南極 \((0,0,-1)\) からの立体射影 \(\varphi:(x,y,z)\mapsto (x+iy)/(1+z)\) による \(P\) の像は

\[\begin{align} \varphi(P) = \frac{\sin\theta}{1+\cos\theta} =\frac{\sqrt{2(1+\cos2\theta)}}{\sin2\theta} -\frac{1+\cos2\theta}{\sin2\theta} =\sqrt{\frac{5+\sqrt{5}}{2}} - \frac{1+\sqrt{5}}{2} \end{align}\]

と決まる．一次分数変換による\(U\) の作用で \(\varphi(P)\) は不変だから，これは \(\phi_1(i)/\phi_2(i)\) に一致していて，再びラマヌジャンの連分数の値が求まった．つまり，ラマヌジャンの連分数は図示するとこうなる：

Figure 1. ラマヌジャンの連分数の幾何学的意味付け．\(V_1\) と　\(V_2\) は辺によって隣接する正二十面体の \(2\) 頂点である．正二十面体は単位球に外接する．

\(e\) と \(\pi\) の現れる連分数と4次の代数的数が保型形式と正二十面体を通して結びつけられた．なかなか感動的ではないだろうか．

ちなみに \(\varphi(P)=\tan(\theta/2)\) は \(30\) 次の（\(1\)変数）正二十面体多項式 \(V_{30}(t,1)\) の根である．\(V_{30}(t,1)\) の他の \(29\)個の根も \(\varphi(P)\) への一次分数変換による二項正二十面体群の作用ですべて得られる．

また, \(\tan(\theta/2)\) の \(\mathbb{Q}\) 上での最小多項式は \(t^4+2\,t^3-6\,t^2-2\,t+1\) だが, これは \(V_{30}(t,1)\) を割り切る．実際，

\[\begin{align} V_{30}(t,1) =& (t^2+1)(t^4+2\,t^3-6\,t^2-2\,t+1)(t^8-t^6+t^4-t^2+1)\\ &\times (t^8-6\,t^7+17\,t^6-18\,t^5+25\,t^4+18\,t^3+17\,t^2+6\,t+1)\\ &\times (t^8+4\,t^7+17\,t^6+22\,t^5+5\,t^4-22\,t^3+17\,t^2-4\,t+1) \end{align}\]

である．ついでに，

\[\begin{align} V_{12}(t,1) &= t(t^2+t-1)(t^4-3\,t^3+4\,t^2-2\,t+1)(t^4+2\,t^3+4\,t^2+3\,t+1),\\ V_{20}(t,1) &= (t^4-3\,t^3-t^2+3\,t+1)(t^8-t^7+7\,t^6+7\,t^5-7\,t^3+7\,t^2+t+1)\\ &\times (t^8+4\,t^7+7\,t^6+2\,t^5+15\,t^4-2\,t^3+7\,t^2-4\,t+1). \end{align}\]

\(V_{12}(t,1)\) の分解は \(R(q)\) の 「五倍公式」，すなわち \(u=R(q^5),\,v=R(q)\) であるとき,

\[\begin{align} v^5 &= u\frac{u^4-3\,u^3+4\,u^2-2\,u+1}{u^4+2\,u^3+4\,u^2+3\,u+1} \end{align}\]

という，これもまたラマヌジャンのハーディ宛の手紙に書かれていた等式と見比べられる．「手紙」に書かれていたもう一つの特殊値である

\[\begin{align} R(\sqrt{5}\,i) = \frac{\sqrt{5}}{1+\sqrt[\leftroot{-2}\uproot{2}5]{5^{3/4}(\frac{\sqrt{5}-1}{2})^{5/2}-1}}-\frac{1+\sqrt{5}}{2} = 0.0602094065\cdots \end{align}\]

という値は \(T\) による変換式とこれを連立させれば出てくるはずだが，幾何学的な意味付けは可能なのだろうか．

レベル5の主合同部分群

ラマヌジャンの連分数に関してはここまでにして，まとめると，

\[\begin{align} \begin{pmatrix} \phi_1(T\tau)\\ \phi_2(T\tau) \end{pmatrix} &= \zeta^3 \begin{pmatrix} \zeta^3 & 0\\ 0 & \zeta^2 \end{pmatrix} \begin{pmatrix} \phi_1(\tau)\\ \phi_2(\tau) \end{pmatrix},\\ \begin{pmatrix} \phi_1(S\tau)\\ \phi_2(S\tau) \end{pmatrix} &= \frac{(-i\tau)^{1/5}}{i\sqrt{5}} \begin{pmatrix} -\zeta+\zeta^4 & \zeta^2-\zeta^3\\ \zeta^2-\zeta^3 & \zeta-\zeta^4 \end{pmatrix} \begin{pmatrix} \phi_1(\tau)\\ \phi_2(\tau) \end{pmatrix} \end{align}\]

と書ける．ここに現れた行列（の逆の定数倍）によって生成される群

\[\begin{align} \left\langle \begin{pmatrix} \zeta^2 & 0\\ 0 & \zeta^3 \end{pmatrix},\, \frac{1}{\sqrt{5}} \begin{pmatrix} -\zeta+\zeta^4 & \zeta^2-\zeta^3\\ \zeta^2-\zeta^3 & \zeta-\zeta^4 \end{pmatrix} \right\rangle \end{align}\]

は位数 \(120\) の二項正二十面体群に他ならない．\(SU(2)\) の元にするために無視した定数因子の寄与もきちんと考慮すると，Shephard and Toddによって分類されたユニタリ鏡映群のうち，No.16という位数600の群になるらしい［Ibukiyama］．

\(\phi_1(\tau), \phi_2(\tau)\) の比は \(\tau\) の関数として \(\Lambda(\tau)\) で定義したが（実態は\(R(q)\)と同じもの），これへの左からの作用は

\[\begin{align} \Lambda(T^{-1}\tau) &= \zeta^4 \Lambda(\tau),\\ \Lambda(S^{-1}\tau) &= \frac{(-\zeta+\zeta^4)\Lambda(\tau)+(\zeta^2-\zeta^3)}{(\zeta^2-\zeta^3)\Lambda(\tau)+(\zeta-\zeta^4)} \end{align}\]

となる．これは，\(\Lambda(\tau)\) への作用として

\[\begin{align} \psi : PSL(2, \mathbb{Z}) &\rightarrow PSL(2,\mathbb{C}),\\ \psi(T) &= z \mapsto \zeta^4 z,\\ \psi(S) &= z \mapsto \frac{(-\zeta+\zeta^4)z+(\zeta^2-\zeta^3)}{(\zeta^2-\zeta^3)z+(\zeta-\zeta^4)} \end{align}\]

という群準同型を与えている．値域は実際には \(\psi(T),\psi(S)\) によって生成される群で，明らかに正二十面体群 \(\cong\) 5次対称群 \(\cong PSL(2,\mathbb{F}_5)\) と同型になる．このうち \(5\) 次対称群への同型写像としては

\[\begin{align} \rho(T) &\mapsto (12345),\\ \rho(S) &\mapsto (12)(34) \end{align}\]

を取ることができる．

このことからも示唆されるように，\(\rho\) の核はレベル5の主合同部分群 \(\Gamma(5)\) の中心による剰余群 \(\overline{\Gamma(5)}\) であることが知られている．そして \(\phi_1(\tau), \phi_2(\tau)\) は この \(\Gamma(5)\) に関するウェイト \(1/5\) の保型形式なのである．興味深いことに，通常の整数ウェイトの \(\Gamma(5)\) に関する保型形式はこの \(2\) つによって生成されるらしい［Ibukiyama 第6章］．

文献［Ibukiyama］ではさらに，\(3\) 以上の奇数 \(N\) に対して 分数ウェイト \((N-3)/2N\) の \(\Gamma(N)\) に関する保形形式の一般論が展開されている．ここには \(N=5\) に留まらない豊かな一般論があるようだ（クラインは \(N=7\) の場合を既に調べていた［Klein2］）．すると，もしかすると「正多面体多項式」を正多面体以外の場合にも拡張することができるのだろうか．

分割数

ここでは主に \(\phi_1, \phi_2\) をベースに論を進めたが，\(g, h\) も十分に良い性質を持っている． 振り返ると，

\[\begin{align} g(\tau) &= q^{-1/60} \prod_{n \equiv \pm 1\!\mod\!5,\, n\geq 1} \frac{1}{1-q^n},\\ h(\tau) &= q^{11/60} \prod_{n \equiv \pm 2\!\mod\!5,\, n\geq 2} \frac{1}{1-q^n} \end{align}\]

であった．\(V_{12}(h(\tau), g(\tau))=-1\) は既に見た通り．では「逆」に入れるとどうなるだろうか（筆者は実際に間違えて逆に入れて計算したときに以下の事実に気付いた）．

\[\begin{align} f(\tau):=V_{12}(g(\tau), h(\tau))=1+22\,q+132\,q^2+594\,q^3+2156\,q^4+6930\,q^5+20064\,q^6+\cdots \end{align}\]

定数項を除いて \(22\) で割り切れる．\(1\) 次の項から順に係数を \(22\) で割った数を列挙すると，

\[\begin{align} 1,\,6,\,27,\,98,\,315,\,912,\cdots \end{align}\]

OEISに最初の \(4\) 項を突っ込む.

どん.

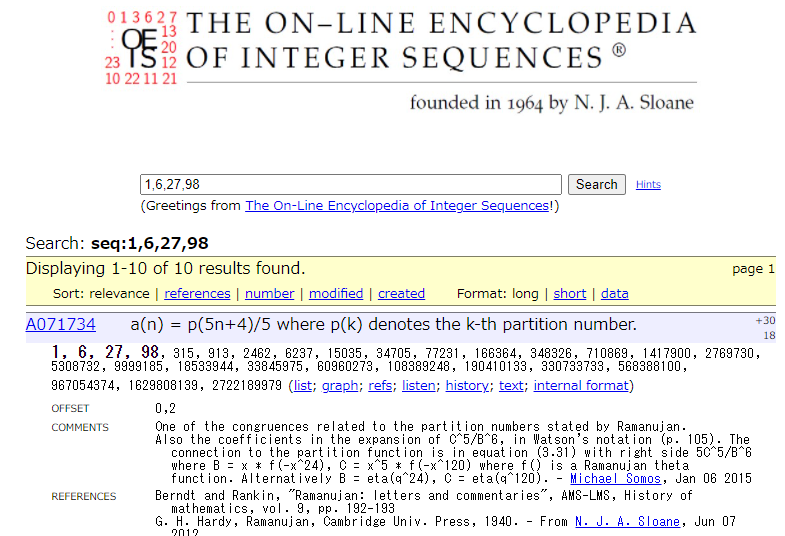
Figure 2. ‘1,6,27.98’をOEISで検索した結果．

またラマヌジャンだ．

ラマヌジャンは分割数 \(p(n)\) に関する次の結果を得た．非負整数 \(n\) に対して，

\[\begin{align} p(5\,n+4) &\equiv 0 \mod 5,\\ p(7\,n+5) &\equiv 0 \mod 7,\\ p(11\,n+6) &\equiv 0 \mod 11. \end{align}\]

（\(5,\,7,\,11\) の並びは ガロアの最後の手紙 を思い出させるしADEっぽさがある．これは何なんだろう）

一番上の式が言っているのは \(p(5n+4)/5\) が整数になるということで，それを順に並べたのが A071734 で登録されている数列である．参考までに下2つの場合も挙げておく．

• \(p(7n+5)/7\) : A071746
• \(p(11n+6)/11\) : A076394

では \(f(\tau)/22\) の係数がこれに一致するかというと，\(5\) 次の項が \(912\) であるのに対して \(p(5\cdot 5+4)/5=912\) でずれている．「補正」を加えてやると，

\[\begin{align} f(\tau) = 1+22\,\left((1-q^5)(1-q^{10})(1-q^{15})\cdots\right)\sum_{n=0}^\infty \frac{p(5n+4)}{5} q^{n+1} \end{align}\]

らしいことが分かる．

\[\begin{align} f(\tau) &= V_{12}(g(\tau),\,h(\tau))\\ &= -V_{12}(h(\tau),\,g(\tau)) + 22 g(\tau)^6 h(\tau)^6 \end{align}\]

だから，

\[\frac{g(\tau)^6h(\tau)^6}{(1-q^5)(1-q^{10})(1-q^{15})\cdots} = \sum_{n=0}^\infty \frac{p(5n+4)}{5} q^{n+1},\]

エータ関数を使うと，

\[q^{-19/24}\frac{\eta(5\tau)^5}{\eta(\tau)^6} = \sum_{n=0}^\infty \frac{p(5n+4)}{5} q^{n+1}\]

となってA071734の”FORMULA”の項にある母関数（G.f）と一致する．ラマヌジャンによる合同関係の証明はこの関係を示すことによっている［Ramanujan2］．

\(V_{20}, V_{30}\) は，

\[\begin{align} V_{20}(h(\tau), g(\tau)) &= \frac{E_4(\tau)}{\eta(\tau)^8}\\ &= q^{-1/3}\left(1+248\,q+4124\,q+34752\,q^3+213126\,q^4+1057504\,q^6+4530744\,q^6+\cdots\right),\\ V_{30}(h(\tau), g(\tau)) &= \frac{E_6(\tau)}{\eta(\tau)^{12}}\\ &= q^{-1/2}\left(1-492\,q-22590\,q^2-367400\,q^3-3764865\,q^4-28951452\,q^5-182474434\,q^6-\cdots\right) \end{align}\]

となって，この係数もまたモンスター群という語が登場していかにも奥が深そうだが，この意味付けは正直自分の理解を完全に超えている．

• A007242 McKay-Thompson series of class 2a for the Monster group.
• A007245 McKay-Thompson series of class 3C for the Monster group.

残念ながら逆に入れた場合の数列は適当な変換をいくつか試しても意味のありそうなヒットはなかった．参考までに最初の \(10\) 項までの係数を挙げておく．

\[\begin{align} \begin{array}{|crr|}\hline n & V_{20}(g(\tau), h(\tau)) & V_{30}(g(\tau), h(\tau)) \\ \hline 0 & 1 & 1\\ 1 & -208 & 552\\ 2 & -2716 & 3510\\ 3 & -21792 & -22880\\ 4 & -131154 & -575445\\ 5 & -645656 & -5707836\\ 6 & -2755224 & -40464334\\ 7 & -10519232 & -234032520\\ 8 & -36768567 & -1172993445\\ 9 & -119480240 & -5269051580\\ \hline \end{array} \end{align}\]

Table 4. \(V_{20}(g,h), V_{30}(g,h)\) の \(q-\)展開係数.

まとめと展望

本記事では正多面体多項式と保型形式との深い繋がりを垣間見た．連分数やロジャース・ラマヌジャンの恒等式のような「有名人」とこの過程で出会うのは思いがけないことであった．

Broué–Enguehard 写像は正八面体群（というよりは位数 \(96\) のユニタリ鏡映群と見るべきのようだけど）の不変式を通じて格子と符号を結びつける．特に，”極限的”（extremal）重偶自己双対多項式の重み枚挙多項式は，これまでの記事で「代表多項式」と呼んでいた多項式と共通の構成法を持ち，やはり係数には特徴的な整除性が見られる．だから多分代表多項式を「極限的正多面体多項式」と呼ぶことは十分正当化されるだろう．

極限的正多面体多項式の係数に素数が現れる意味は何故か？　大きな関心はやはりそこにある．これを解釈するために「正二十面体版」のBroué–Enguehard 写像はどんな意味を持つのだろうか．もっとも，組合せ論的であろうとなかろうと整除性を示す方が先にあるべきだろうけれど…….　まあともかく，この正二十面体から拡がる世界を色々見ていきたい．

References

• ［Zagier］Max Planck研究所のDon Zagierによる講義シリーズ “The Rogers-Ramanujan identities and the icosahedron”の録画映像．本記事の内容はこの動画によるところが大きい（開催時期と概要が異なるこれとの関係はなんだろう．）． Lecture 1, Lecture 2, Lecture 3, Lecture 4
• ［Klein1］F. クライン（関口次郎，前田博信 訳）『正20面体と5次方程式（改訂新版）』（2012年，丸善出版）
• ［Ibukiyama］伊吹山知義『保型形式特論』（2018年，共立出版）
• ［Bannai］坂内英一，坂内悦子，伊藤達郎『代数的組合せ論入門』（2016年，共立出版）
• ［Yamada1］山田裕史『組合せ論プロムナード』（2009年，日本評論社）
• ［Yamada2］山田裕史，”ロジャーズ-ラマヌジャン恒等式 (特集 整数の分割).” 数学セミナー 56.2 (2017): 23-27.
• ［Koblitz］N. コブリッツ（上田勝，浜畑芳紀 訳）『楕円曲線と保型形式』（丸善出版，2012年）
• ［Andrews］ジョージ・アンドリュース，キムモ・エリクソン（佐藤文広 訳）『整数の分割』（数学書房，2006年）
• ［Andrews2］ Andrews, George E., and Bruce C. Berndt. Ramanujan’s lost notebook. Vol. 1. New York: Springer, 2005.
• ［Takase］髙瀬幸一，”ラマヌジャン登場 (ラマヌジャン: 現代数理科学に生きる業績と着想).” 数理科学 58.8 (2020): 5-7.
• ［Tsuchioka］土岡俊介，”アフィン・リー環とロジャーズ-ラマヌジャン恒等式 (ラマヌジャン: 現代数理科学に生きる業績と着想).” 数理科学 58.8 (2020): 54-59.
• ［Harada］原田昌晃， “72 次元の極値偶ユニモジュラー格子の存在について (特集 ［想定外］ の数学).” 数学セミナー 51.1 (2012): 13-17.
• ［Conway］J. H. Conway, and N. J. A. Sloane, “Sphere packings, lattices and groups”, Vol. 290. Springer Science & Business Media （2013）.　特に第7章 “Further Connections Between Codes and Lattices”.
• ［Kharchev］S. Kharchev, and A. Zabrodin. “Theta vocabulary I.” Journal of Geometry and Physics 94 (2015): 19-31. https://doi.org/10.1016/j.geomphys.2015.03.010
• ［Duke］ W. Duke, “Continued fractions and modular functions.” Bulletin of the American Mathematical Society 42.2 (2005): 137-162. https://www.math.ucla.edu/~wdduke/preprints/bams4.pdf
• ［Nash］ O. Nash, “On Klein’s icosahedral solution of the quintic.” Expositiones Mathematicae 32.2 (2014): 99-120.https://www.math.ucla.edu/~wdduke/preprints/bams4.pdf　著者のウェブサイト
• ［Kaneko1］金子昌信, “ある微分方程式を満たすモジュラー形式について (解析的整数論とその周辺).” 数理解析研究所講究録 1384 (2004): 50-56.https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/25731/1/1384-8.pdf
• ［Kaneko2］M. Kaneko, “On modular forms of weight (6n+ 1)/5 satisfying a certain differential equation.” Number theory. Springer, Boston, MA, (2006): 97-102.https://www2.math.kyushu-u.ac.jp/~mkaneko/papers/wtfifth.pdf
• ［Hashimoto1］橋本義武, 『正多面体と素数』（2021年，放送大学教育振興会）
• ［Hashimoto2］橋本義武, “正 20 面体方程式 (特集 クラインの見た正 20 面体).” 数学セミナー 46.1 (2007): 26-29.
• ［Sekiguchi1］関口次郎, 『正20面体群からの旅たち』https://www.math.chuo-u.ac.jp/ENCwMATH/51/ewm51_Sekiguchi1.pdf
• ［Sekiguchi2］関口次郎，『クラインとポアンカレの往復書簡について――保型関数論の源流』https://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo14/14_4sekiguchi.pdf
• ［Shiga1］志賀弘典, “正 20 面体方程式と超幾何函数 (特集 クラインの見た正 20 面体).” 数学セミナー 46.1 (2007): 30-33.
• ［Shiga2］志賀弘典，『保型関数　古典理論とその現代的応用』（2017年，共立出版）
• ［Ranamujan1］S. Ramanujan, “Algebraic relations between certain infinite products.” Proc. London Math. Soc 2 (1920): 18.https://www.imsc.res.in/~rao/ramanujan/CamUnivCpapers/Cpaper29/page1.htm
• ［Ramanujan2］S. Ramanujan, “Algebraic relations between certain infinite products.” Proc. London Math. Soc 2 (1920): 18.https://www.imsc.res.in/~rao/ramanujan/CamUnivCpapers/Cpaper29/page1.htm
• ［Klein2］ Klein, Felix. “Ueber die Transformation siebenter Ordnung der elliptischen Functionen.” Mathematische Annalen 14.3 (1878): 428-471.https://doi.org/10.1007/BF01677143 （On the Order-Seven Transformation of Elliptic Functions）